What statistic is to be used?
The statistic object defines the numerical quantity which describes the “quality” of the fit, where the definition is that as the statistic value decreases, the model is getting to better describe the data. It is the statistic value that the optimiser uses to determine the “best-fit” parameter settings.
A simple example is the least-squares statistic which, if the data
and model points are \(d_i\) and \(m_i\) respectively,
where the suffix indicates the bin number, then the overall
statistic value is \(s = \sum_i (d_i - m_i)^2\). This is
provided by the LeastSq class, and
an example of its use is shown below. First we import the
classes we need:
>>> import numpy as np
>>> from sherpa.data import Data1D
>>> from sherpa.models.basic import Gauss1D
>>> from sherpa.stats import LeastSq
As the data I use a one-dimensional gaussian with normally-distributed noise:
>>> np.random.seed(0)
>>> x = np.linspace(-5., 5., 200)
>>> gmdl = Gauss1D()
>>> gmdl.fwhm = 1.9
>>> gmdl.pos = 1.3
>>> gmdl.ampl = 3
>>> y = gmdl(x) + np.random.normal(0., 0.2, x.shape)
>>> d = Data1D('stat-example', x, y)
The statistic value, along with per-bin values, is returned by
the calc_stat() method, so we
can find the statistic value of this parameter set with:
>>> stat = LeastSq()
>>> s = stat.calc_stat(d, mdl)
>>> print("Statistic value = {}".format(s[0]))
Statistic value = 8.38666216358492
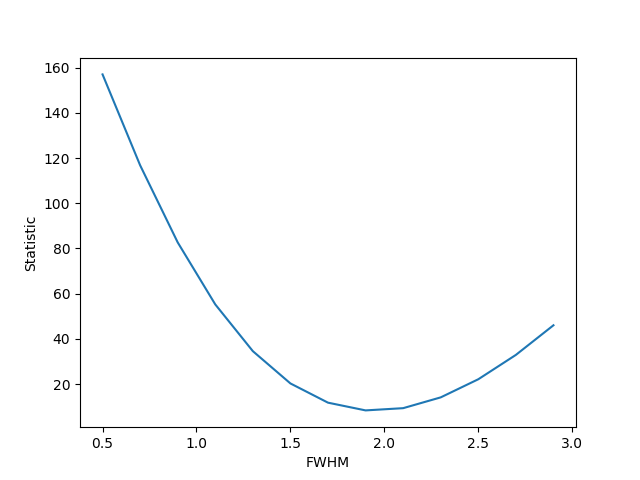
As the FWHM is varied about the true value we can see that the statistic increases:
>>> fwhm = np.arange(0.5, 3.0, 0.2)
>>> sval = []
>>> for f in fwhm:
... gmdl.fwhm = f
... sval.append(stat.calc_stat(d, gmdl)[0])
...
>>> plt.plot(fwhm, sval)
>>> plt.xlabel('FWHM')
>>> plt.ylabel('Statistic')
The statistic classes provided in Sherpa are given below, and cover a range of possibilities, such as: least-square for when there is no knowledge about the errors on each point, a variety of chi-square statistics for when the errors are assumed to be gaussian, and a variety of maximum-likelihood estimators for Poisson-distributed data. It is also possible to add your own statistic class.