Markov Chain Monte Carlo and Poisson data¶
Sherpa provides a Markov Chain Monte Carlo (MCMC) method designed for Poisson-distributed data. It was originally developed as the Bayesian Low-Count X-ray Spectral (BLoCXS) package, but has since been incorporated into Sherpa. It is developed from the work presented in Analysis of Energy Spectra with Low Photon Counts via Bayesian Posterior Simulation by van Dyk et al.
Unlike many MCMC implementations, idea is that have some idea of the search surface at the optimum - i.e. the covariance matrix - and then use that to explore this region.
Example¶
Note
This example probably needs to be simplified to reduce the run time
Simulate the data¶
Create a simulated data set:
>>> np.random.seed(2)
>>> x0low, x0high = 3000, 4000
>>> x1low, x1high = 4000, 4800
>>> dx = 15
>>> x1, x0 = np.mgrid[x1low:x1high:dx, x0low:x0high:dx]
Convert to 1D arrays:
>>> shape = x0.shape
>>> x0, x1 = x0.flatten(), x1.flatten()
Create the model used to simulate the data:
>>> from sherpa.astro.models import Beta2D
>>> truth = Beta2D()
>>> truth.xpos, truth.ypos = 3512, 4418
>>> truth.r0, truth.alpha = 120, 2.1
>>> truth.ampl = 12
Evaluate the model to calculate the expected values:
>>> mexp = truth(x0, x1).reshape(shape)
Create the simulated data by adding in Poisson-distributed noise:
>>> msim = np.random.poisson(mexp)
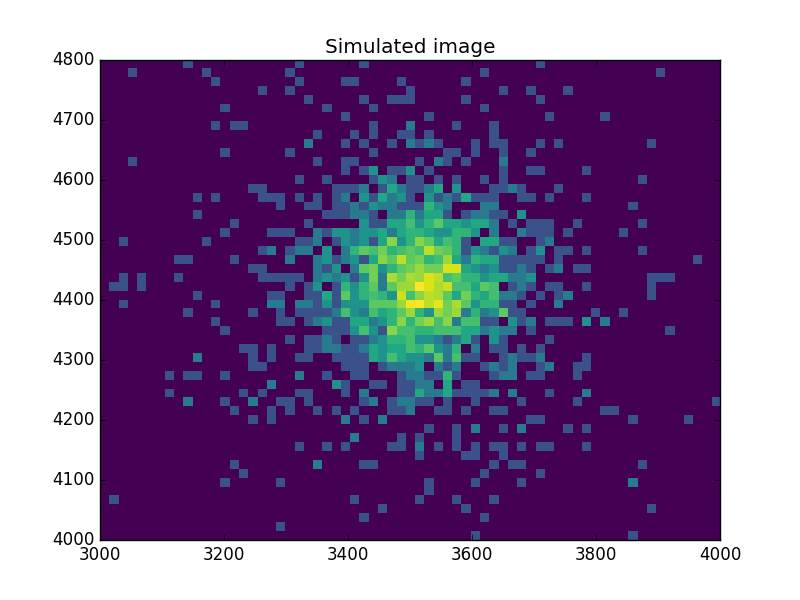
What does the data look like?¶
Use an arcsinh transform to view the data, based on the work of Lupton, Gunn & Szalay (1999).
>>> plt.imshow(np.arcsinh(msim), origin='lower', cmap='viridis',
...: extent=(x0low, x0high, x1low, x1high),
...: interpolation='nearest', aspect='auto')
>>> plt.title('Simulated image')
Find the starting point for the MCMC¶
Set up a model and use the standard Sherpa approach to find a good starting place for the MCMC analysis:
>>> from sherpa import data, stats, optmethods, fit
>>> d = data.Data2D('sim', x0, x1, msim.flatten(), shape=shape)
>>> mdl = Beta2D()
>>> mdl.xpos, mdl.ypos = 3500, 4400
Use a Likelihood statistic and Nelder-Mead algorithm:
>>> f = fit.Fit(d, mdl, stats.Cash(), optmethods.NelderMead())
>>> res = f.fit()
>>> print(res.format())
Method = neldermead
Statistic = cash
Initial fit statistic = 20048.5
Final fit statistic = 607.229 at function evaluation 777
Data points = 3618
Degrees of freedom = 3613
Change in statistic = 19441.3
beta2d.r0 121.945
beta2d.xpos 3511.99
beta2d.ypos 4419.72
beta2d.ampl 12.0598
beta2d.alpha 2.13319
Now calculate the covariance matrix (the default error estimate):
>>> f.estmethod
<Covariance error-estimation method instance 'covariance'>
>>> eres = f.est_errors()
>>> print(eres.format())
Confidence Method = covariance
Iterative Fit Method = None
Fitting Method = neldermead
Statistic = cash
covariance 1-sigma (68.2689%) bounds:
Param Best-Fit Lower Bound Upper Bound
----- -------- ----------- -----------
beta2d.r0 121.945 -7.12579 7.12579
beta2d.xpos 3511.99 -2.09145 2.09145
beta2d.ypos 4419.72 -2.10775 2.10775
beta2d.ampl 12.0598 -0.610294 0.610294
beta2d.alpha 2.13319 -0.101558 0.101558
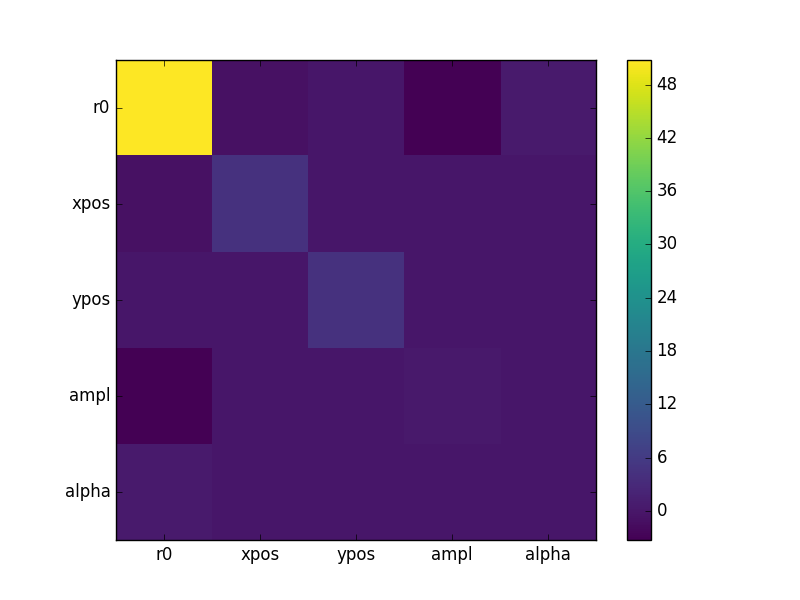
The covariance matrix is stored in the extra_output attribute:
>>> cmatrix = eres.extra_output
>>> pnames = [p.split('.')[1] for p in eres.parnames]
>>> plt.imshow(cmatrix, interpolation='nearest', cmap='viridis')
>>> plt.xticks(np.arange(5), pnames)
>>> plt.yticks(np.arange(5), pnames)
>>> plt.colorbar()
Run the chain¶
Finally, run a chain (use a small number to keep the run time low for this example):
>>> from sherpa.sim import MCMC
>>> mcmc = MCMC()
>>> mcmc.get_sampler_name()
>>> draws = mcmc.get_draws(f, cmatrix, niter=1000)
>>> svals, accept, pvals = draws
>>> pvals.shape
(5, 1001)
>>> accept.sum() * 1.0 / 1000
0.48499999999999999
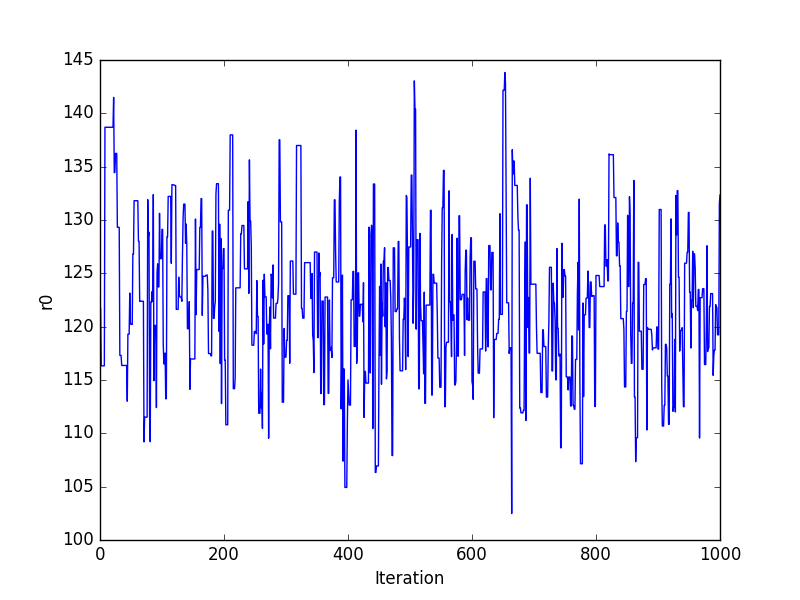
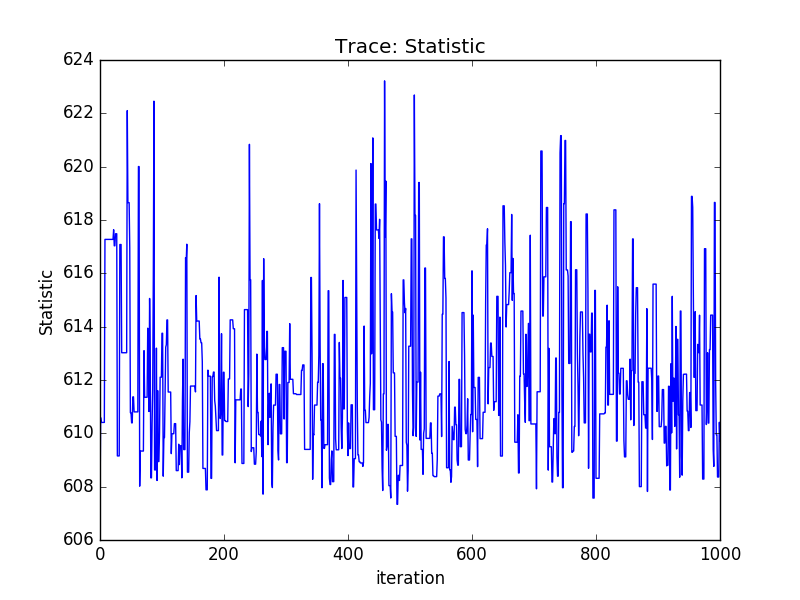
Trace plots¶
>>> plt.plot(pvals[0, :])
>>> plt.xlabel('Iteration')
>>> plt.ylabel('r0')
Or using the sherpa.plot module:
>>> from sherpa import plot
>>> tplot = plot.TracePlot()
>>> tplot.prepare(svals, name='Statistic')
>>> tplot.plot()
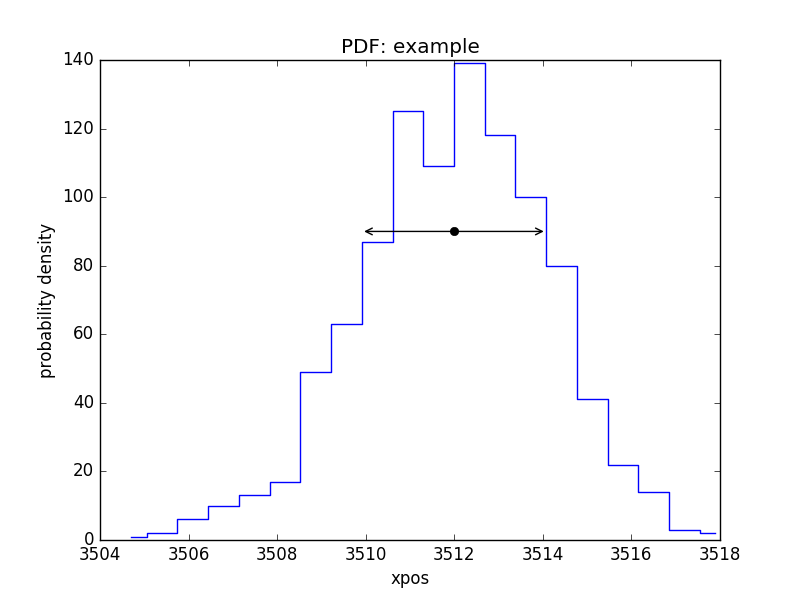
PDF of a parameter¶
>>> pdf = plot.PDFPlot()
>>> pdf.prepare(pvals[1, :], 20, False, 'xpos', name='example')
>>> pdf.plot()
Add in the covariance estimate:
>>> xlo, xhi = eres.parmins[1] + eres.parvals[1], eres.parmaxes[1] + eres.parvals[1]
>>> plt.annotate('', (xlo, 90), (xhi, 90), arrowprops={'arrowstyle': '<->'})
>>> plt.plot([eres.parvals[1]], [90], 'ok')
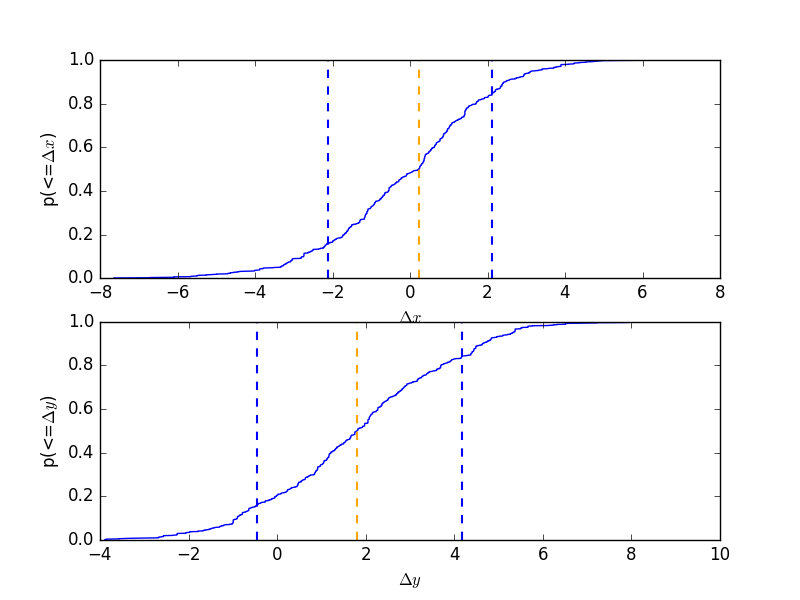
CDF for a parameter¶
Normalise by the actual answer to make it easier to see how well the results match reality:
>>> cdf = plot.CDFPlot()
>>> plt.subplot(2, 1, 1)
>>> cdf.prepare(pvals[1, :] - truth.xpos.val, r'$\Delta x$')
>>> cdf.plot(clearwindow=False)
>>> plt.title('')
>>> plt.subplot(2, 1, 2)
>>> cdf.prepare(pvals[2, :] - truth.ypos.val, r'$\Delta y$')
>>> cdf.plot(clearwindow=False)
>>> plt.title('')
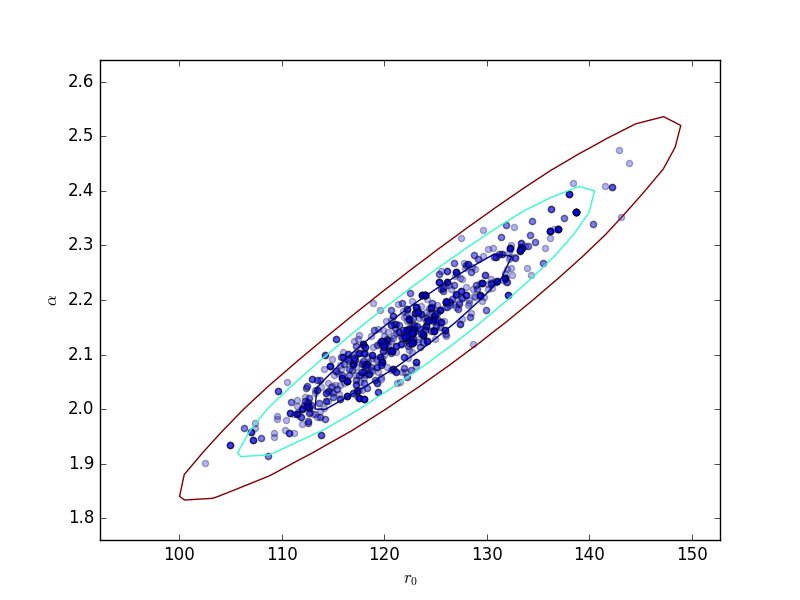
Scatter plot¶
>>> plt.scatter(pvals[0, :] - truth.r0.val,
...: pvals[4, :] - truth.alpha.val, alpha=0.3)
>>> plt.xlabel(r'$\Delta r_0$', size=18)
>>> plt.ylabel(r'$\Delta \alpha$', size=18)
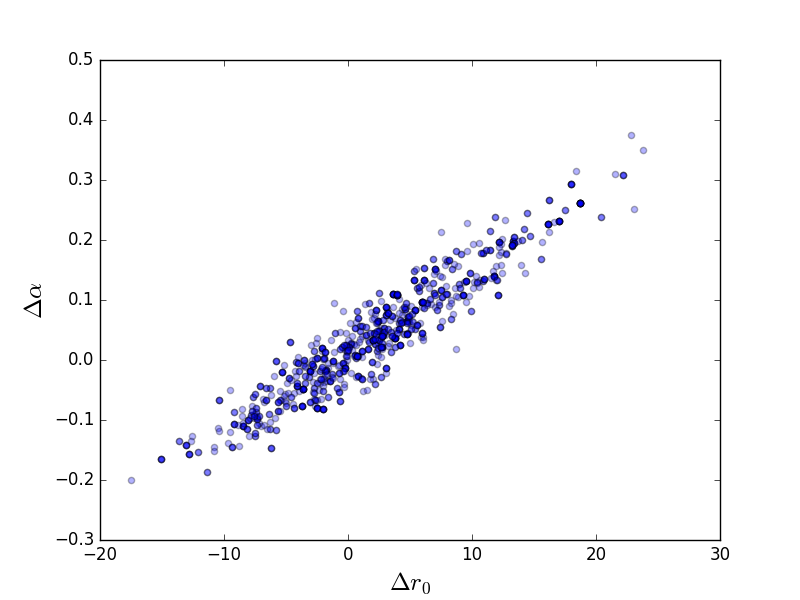
This can be compared to the
RegionProjection calculation:
>>> plt.scatter(pvals[0, :], pvals[4, :], alpha=0.3)
>>> from sherpa.plot import RegionProjection
>>> rproj = RegionProjection()
>>> rproj.prepare(min=[95, 1.8], max=[150, 2.6], nloop=[21, 21])
>>> rproj.calc(f, mdl.r0, mdl.alpha)
>>> rproj.contour(overplot=True)
>>> plt.xlabel(r'$r_0$'); plt.ylabel(r'$\alpha$')